Como a nova arquitetura BitNet da Microsoft está impulsionando a eficiência de LLMs

Modelos de linguagem de um bit (LLMs) surgiram como uma abordagem promissora para tornar a IA generativa mais acessível e econômica. Ao representar os pesos do modelo com um número muito limitado de bits, os LLMs de 1 bit reduzem drasticamente os recursos de memória e computação necessários para executá-los.

A Pesquisa da Microsoft tem pressionado os limites dos LLMs de 1 bit com sua arquitetura BitNet. Em um novo artigo, os pesquisadores apresentam o BitNet a4.8, uma nova técnica que melhora ainda mais a eficiência dos LLMs de 1 bit sem sacrificar seu desempenho.

A ascensão dos LLMs de 1 bit

Os LLMs tradicionais utilizam números de ponto flutuante de 16 bits (FP16) para representar seus parâmetros. Isso requer muita memória e recursos computacionais, o que limita a acessibilidade e as opções de implementação para LLMs. Os LLMs de 1 bit abordam esse desafio reduzindo drasticamente a precisão dos pesos do modelo, mantendo o desempenho dos modelos de precisão total.

Modelos anteriores do BitNet usavam valores de 1,58 bits (-1, 0, 1) para representar pesos do modelo e valores de 8 bits para ativações. Essa abordagem reduziu significativamente os custos de memória e E/S, mas o custo computacional das multiplicações de matrizes permaneceu um gargalo, e otimizar redes neurais com parâmetros de bits extremamente baixos é desafiador.

Duas técnicas ajudam a enfrentar esse problema. A esparsificação reduz o número de cálculos ao podar ativações com magnitudes menores. Isso é particularmente útil nos LLMs, pois os valores de ativação tendem a ter uma distribuição de cauda longa, com alguns valores muito grandes e muitos pequenos.

A quantização, por outro lado, utiliza um número menor de bits para representar ativações, reduzindo o custo computacional e de memória do processamento delas. No entanto, simplesmente reduzir a precisão das ativações pode resultar em erros de quantização significativos e degradação do desempenho.

Além disso, combinar esparsificação e quantização é desafiador e apresenta problemas especiais ao treinar LLMs de 1 bit.

“Tanto a quantização quanto a esparsificação introduzem operações não diferenciáveis, o que torna o cálculo do gradiente durante o treinamento particularmente desafiador,” disse Furu Wei, Gerente de Pesquisa Parceiro da Microsoft Research, ao VentureBeat.

O cálculo do gradiente é essencial para calcular erros e atualizar parâmetros ao treinar redes neurais. Os pesquisadores também precisaram garantir que suas técnicas pudessem ser implementadas eficientemente no hardware existente, mantendo os benefícios da esparsificação e da quantização.

BitNet a4.8

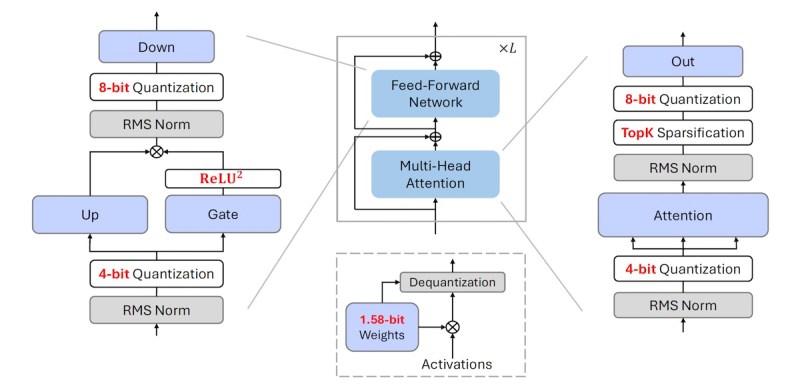
O BitNet a4.8 enfrenta os desafios de otimização dos LLMs de 1 bit através do que os pesquisadores descrevem como “quantização e esparsificação híbridas.” Eles conseguiram isso projetando uma arquitetura que aplica seletivamente a quantização ou a esparsificação a diferentes componentes do modelo com base no padrão de distribuição específico das ativações. A arquitetura utiliza ativações de 4 bits para entradas nos níveis de atenção e na rede de avanço (FFN). Usa esparsificação com 8 bits para estados intermediários, mantendo apenas os 55% principais dos parâmetros. A arquitetura também é otimizada para tirar proveito do hardware existente.

“Com o BitNet b1.58, o gargalo de inferência dos LLMs de 1 bit muda de memória/E/S para computação, que é limitada pelos bits de ativação (ou seja, 8 bits no BitNet b1.58),” disse Wei. “No BitNet a4.8, reduzimos os bits de ativação para 4 bits para que possamos aproveitar os kernels de 4 bits (por exemplo, INT4/FP4) e trazer um aumento de 2x na inferência de LLMs em dispositivos GPU. A combinação de pesos do modelo de 1 bit do BitNet b1.58 e ativações de 4 bits do BitNet a4.8 efetivamente aborda tanto as limitações de memória/E/S quanto as de computação na inferência de LLMs.”

O BitNet a4.8 também utiliza valores de 3 bits para representar os estados de chave (K) e valor (V) no mecanismo de atenção. O cache KV é um componente crucial dos modelos de transformadores. Ele armazena as representações dos tokens anteriores na sequência. Ao reduzir a precisão dos valores do cache KV, o BitNet a4.8 reduz ainda mais os requisitos de memória, especialmente ao lidar com sequências longas.

A promessa do BitNet a4.8

Resultados experimentais mostram que o BitNet a4.8 oferece desempenho comparável ao seu predecessor BitNet b1.58 enquanto utiliza menos computação e memória.

Comparado aos modelos Llama de precisão total, o BitNet a4.8 reduz o uso de memória em um fator de 10 e alcança uma aceleração de 4 vezes. Em comparação com o BitNet b1.58, ele alcança uma aceleração de 2 vezes através de kernels de ativação de 4 bits. No entanto, o design pode oferecer muito mais.

“A melhoria estimada na computação é baseada no hardware existente (GPU),” disse Wei. “Com hardware especificamente otimizado para LLMs de 1 bit, as melhorias computacionais podem ser significativamente aumentadas. O BitNet introduz um novo paradigma de computação que minimiza a necessidade de multiplicação de matrizes, um foco principal na otimização do design do hardware atual.”

A eficiência do BitNet a4.8 torna-o particularmente adequado para a implantação de LLMs na borda e em dispositivos com recursos limitados. Isso pode ter importantes implicações para privacidade e segurança. Ao possibilitar LLMs em dispositivos, os usuários podem se beneficiar do poder desses modelos sem precisar enviar seus dados para a nuvem.

Wei e sua equipe continuam seu trabalho em LLMs de 1 bit.

“Continuamos a avançar em nossa pesquisa e visão para a era dos LLMs de 1 bit,” disse Wei. “Enquanto nosso foco atual está na arquitetura do modelo e no suporte ao software (ou seja, bitnet.cpp), pretendemos explorar o co-design e a co-evolução da arquitetura do modelo e do hardware para desbloquear totalmente o potencial dos LLMs de 1 bit.”