Como a escalabilidade em tempo de teste desbloqueia habilidades de raciocínio ocultas em pequenos modelos de linguagem (e permite que superem LLMs)

Modelos de linguagem muito pequenos (SLMs) podem superar os principais modelos de linguagem grandes (LLMs) em tarefas de raciocínio, de acordo com um novo estudo do Laboratório de IA de Xangai. Os autores mostram que, com as ferramentas apropriadas e técnicas de escalonamento em tempo de teste, um SLM com 1 bilhão de parâmetros pode superar um LLM de 405B em benchmarks matemáticos complexos.

A capacidade de implantar SLMs em tarefas complexas de raciocínio pode ser muito útil, já que as empresas estão em busca de novas maneiras de utilizar esses novos modelos em diferentes ambientes e aplicações.

Explicação do escalonamento em tempo de teste

O escalonamento em tempo de teste (TTS) é o processo de oferecer ciclos computacionais extras aos LLMs durante a inferência para melhorar seu desempenho em várias tarefas. Modelos de raciocínio de ponta, como OpenAI o1 e DeepSeek-R1, utilizam “TTS interno”, o que significa que eles são treinados para “pensar” lentamente, gerando uma longa sequência de tokens de cadeia de raciocínio (CoT).

Uma abordagem alternativa é o “TTS externo”, onde o desempenho do modelo é aprimorado com (como o nome sugere) ajuda externa. O TTS externo é adequado para reaproveitar modelos existentes para tarefas de raciocínio sem precisar de um novo ajuste fino. Uma configuração de TTS externo geralmente é composta por um “modelo de política”, que é o principal LLM gerando a resposta, e um modelo de recompensa de processo (PRM) que avalia as respostas do modelo de política. Esses dois componentes são acoplados através de um método de amostragem ou busca.

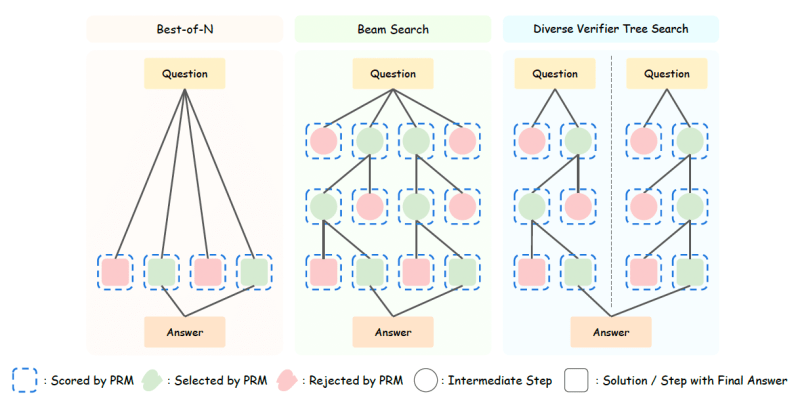
A configuração mais simples é “melhor de-N”, onde o modelo de política gera várias respostas e o PRM seleciona uma ou mais das melhores respostas para compor a resposta final. Métodos de TTS externo mais avançados usam busca. Em “busca em feixe”, o modelo divide a resposta em várias etapas.

Para cada etapa, ele amostra várias respostas e as submete ao PRM. Em seguida, escolhe um ou mais candidatos adequados e gera a próxima etapa da resposta. E, na “busca em árvore de verificação diversificada” (DVTS), o modelo gera vários ramos de respostas para criar um conjunto mais diversificado de respostas candidatas antes de sintetizá-las em uma resposta final.

Qual é a estratégia de escalonamento correta?

Escolher a estratégia de TTS correta depende de múltiplos fatores. Os autores do estudo realizaram uma investigação sistemática sobre como diferentes modelos de política e PRMs afetam a eficiência dos métodos de TTS.

Os resultados mostram que a eficiência depende amplamente dos modelos de política e PRM. Por exemplo, para pequenos modelos de política, métodos baseados em busca superam o melhor de-N. No entanto, para grandes modelos de política, o melhor de-N é mais eficaz porque os modelos têm melhores capacidades de raciocínio e não precisam de um modelo de recompensa para verificar cada etapa de seu raciocínio.

Os resultados também mostram que a estratégia de TTS correta depende da dificuldade do problema. Por exemplo, para pequenos modelos de política com menos de 7B de parâmetros, o melhor de-N funciona melhor em problemas fáceis, enquanto a busca em feixe funciona melhor para problemas mais difíceis. Para modelos de política que têm entre 7B e 32B de parâmetros, a busca em árvore diversificada funciona bem para problemas fáceis e médios, e a busca em feixe é a melhor para problemas difíceis. Mas para grandes modelos de política (72B de parâmetros ou mais), o melhor de-N é o método ideal para todos os níveis de dificuldade.

Por que modelos pequenos podem superar modelos grandes

Com base nesses resultados, os desenvolvedores podem criar estratégias de TTS otimizadas para computação que levam em conta o modelo de política, PRM e a dificuldade do problema para fazer o melhor uso do orçamento computacional para resolver problemas de raciocínio.

Por exemplo, os pesquisadores descobriram que um modelo Llama-3.2-3B com a estratégia de TTS otimizada em termos de computação supera o Llama-3.1-405B em MATH-500 e AIME24, dois benchmarks matemáticos complicados. Isso mostra que um SLM pode superar um modelo que é 135X maior ao usar a estratégia de TTS otimizada em termos de computação.

Em outros experimentos, foi constatado que um modelo Qwen2.5 com 500 milhões de parâmetros pode superar o GPT-4o com a estratégia de TTS otimizada em termos de computação. Usando a mesma estratégia, a versão destilada de 1.5B do DeepSeek-R1 superou o o1-preview e o o1-mini em MATH-500 e AIME24.

Considerando tanto o orçamento de computação de treinamento quanto o de inferência, os resultados mostram que, com estratégias de escalonamento otimizadas para computação, os SLMs podem superar modelos maiores com 100-1000X menos FLOPS.

Os resultados dos pesquisadores mostram que um TTS otimizado para computação melhora significativamente as capacidades de raciocínio dos modelos de linguagem. No entanto, à medida que o modelo de política cresce, a melhoria do TTS diminui gradualmente.

“Isso sugere que a eficácia do TTS está diretamente relacionada à capacidade de raciocínio do modelo de política”, escrevem os pesquisadores. “Especificamente, para modelos com capacidades de raciocínio fracas, escalar a computação em tempo de teste leva a uma melhoria substancial, enquanto para modelos com fortes capacidades de raciocínio, o ganho é limitado.”

O estudo valida que os SLMs podem ter um desempenho melhor do que modelos maiores ao aplicar métodos de escalonamento em tempo de teste otimizados para computação. Embora este estudo se concentre em benchmarks matemáticos, os pesquisadores pretendem expandir suas investigações para outras tarefas de raciocínio, como programação e química.